摘要：跷跷板原理作为一种物理现象，在实际生活中有着广泛的应用。其原理相同的应用体现在多个领域，如工程建筑、机械操作、航空航天等。这种原理的应用不仅丰富了人们的生活体验，还在诸多领域中发挥着重要作用，对社会科技进步产生了深远影响。通过深入了解跷跷板原理的应用及其广泛影响，可以更好地理解物理学与实际生活的紧密联系。

本文目录导读：

1. 杠杆原理
2. 机械装置中的应用
3. 工程领域的应用
4. 自然现象的启示
5. 生物学领域的启示
6. 社会现象中的类比
7. 展望
8. 附录

跷跷板，这个我们小时候经常玩的简单玩具，其实蕴含了丰富的物理学原理，它的上下摆动，实际上是一种机械原理的应用，与许多日常生活中的现象有着惊人的相似性，哪些事物与跷跷板原理相同呢？本文将为您揭示这些事物的奥秘。

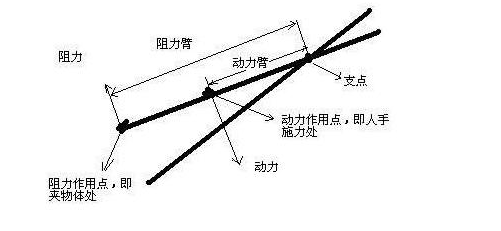
杠杆原理

跷跷板的核心原理是杠杆原理，即力的作用与力臂的乘积相等，类似地，生活中有许多事物都运用了杠杆原理，秤砣、剪刀、扳手、撬棍等，这些工具的设计都是为了实现力的放大或转移，从而达到预期的效果。

机械装置中的应用

除了日常生活中的工具，许多机械装置也运用了与跷跷板相似的原理，汽车的离合器、自行车的刹车系统、齿轮的传动等，这些装置都是通过杠杆原理或其他相关机械原理，实现能量的传递和转换。

工程领域的应用

在工程领域，与跷跷板原理相同的应用更是广泛，桥梁、建筑、道路等的设计都涉及到了结构力学的知识，而结构力学中的许多原理都与杠杆原理相似，通过合理设计结构，可以实现力的传递、分布和平衡，从而确保结构的安全性和稳定性。

自然现象的启示

许多自然现象也与跷跷板原理相同，荡秋千、钟摆的摆动、潮汐的涨落等，这些现象都涉及到力学原理，尤其是杠杆原理和振荡原理的应用，通过对这些现象的研究，可以加深对物理学的理解，发现新的应用前景。

生物学领域的启示

生物学领域也有许多与跷跷板原理相同的现象，肌肉收缩、骨骼杠杆系统等，这些生物力学现象都与杠杆原理有着紧密的联系，通过研究这些现象，可以揭示生命的奥秘，为医学和生物学的发展提供新的思路和方法。

社会现象中的类比

在社会生活中，也有一些现象与跷跷板原理相同，经济领域的供需平衡、政治领域的权力博弈等，这些现象都涉及到一种平衡状态的调整和维护，可以通过杠杆原理进行类比和分析。

与跷跷板原理相同的事物非常广泛，包括杠杆工具、机械装置、工程结构、自然现象、生物学领域以及社会现象等，这些事物都涉及到力学原理的应用，尤其是杠杆原理和振荡原理，通过对这些事物的研究，可以加深对物理学的理解，发现新的应用前景，为相关领域的发展提供新的思路和方法。

展望

随着科技的发展和社会的进步，与跷跷板原理相同的事物将会越来越多，我们可以在更多领域发现力学原理的应用，探索新的技术和方法，我们也需要加强对物理学和相关领域的研究和投入，培养更多具有创新精神和实践能力的人才，为相关领域的发展做出更大的贡献。

附录

为了更好地理解与跷跷板原理相同的事物，我们列举了一些实例：秤砣、剪刀、扳手、撬棍、汽车的离合器、自行车的刹车系统、齿轮的传动、桥梁、建筑、道路的设计、荡秋千、钟摆的摆动、潮汐的涨落、肌肉收缩、骨骼杠杆系统等，这些实例涵盖了多个领域，可以帮助我们更加全面地理解跷跷板原理的广泛应用。